梳理了前面三角基本概念,單位制,扇形與弧長公式,相信大家對三角的學習有了一個好的開始,要想真正的理解三角函式的內涵,還需要從一些口訣來入手,今天我們就來談談三角函式和誘導公式;
第一、三角函式的定義
三角函式的定義分初中(銳角三角比)高中(任意角三角函式),不同的學習階段,對應不同的領悟層次需要。高中階段主要研究的是正餘弦正切函式,因此這三者定義以及函式影象及性質需要完全透徹的理解。

這些三角函式值在各個象限的符號如下圖所示,

記憶的過程中可以結合三角函式函式線的定義以及動態來觀察角α變化的過程中三角函式線的增長趨勢。
第二、三角函式線
角α的三角函式值可以用單位圓的有向線段表示:sinα=MP,cosα=OM,tanα=AT.
有向線段MP,OM,AT分別叫做角α的正弦線,餘弦線,正切線。

對於三角函式線的認知,我們需要關注以下幾點:
(1)結合象限角以及有向線段在各個區間內分別討論,而且需要注意三角函式線中的字母順序不可顛倒,與座標軸方向一致的有向線段為正,此時相應的三角函式值為正,與座標軸方向相反的有向線段為負,對應的三角函式值為負。
(2)當角α的終邊在x軸上時,正切線、正弦線變為一個點,角α的終邊在y軸上時,餘弦線變為一個點,正切線不存在。
(3)若果0<α<π/2,則sinα<α<tanα,sinα+cosα>1。
第三、同角三角基本關係式
針對同一個角,結合三角比的定義,我們會發現,他有如下三種關係:
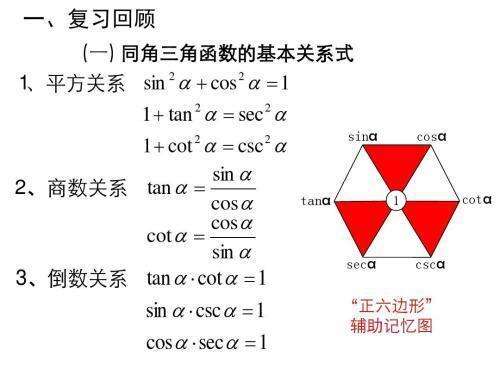
針對上述正六邊形,結合6個三角比,我們藉助:“上弦,中切,下割,左正,右餘,中間1”,這十三字,我們可以很快做好定位,不清楚的同學,可以評論區裡留言。
具體如何應用這正六邊形輔助記憶呢?
首先我們來看平方關係,上圖3個紅色陰影部分,大家可以視為3個倒三角,上底邊的2個三角比的平方之和等於下底角的平方。
其次我們來看商數關係,看相鄰三點,如下圖,再結合上圖,無論ABC,還是ABF,底邊上的2個端點之任意一個端點,都等於中間頂點去除另外一個底點,如:tanα=sinα/cosα,cosα=sinα/tanα,secα=tanα/sinα,cscα=secα/tanα等等;

最後我們再看倒數關係,我們來找正六邊形的對角線,對角線的兩個端點的乘積就是中間1,構成了我們的倒數關係。
以上3個點,我們也可以用一段話來詮釋:
對角線上兩函式之積為1,任一角的函式等於與其相鄰的兩個函式的積,陰影三角形,頂角的兩個函式的平方和等於底角函式的平方。
熟悉了同角三角關係式,在應用的過程中,我們還需要注意以下幾點:三角函式值間的知一求二,或者求式子的值;化簡三角函式式,證明三角恆等式等等。
第四、誘導公式:奇變偶不變,符號看象限

看了上圖的表格,相信大家依然懵懂,不要緊,我們看看這個奇和偶,他是針對π/2,而言的,符號看的是左邊原始式子,對於α,無論大小,均視為銳角,瞭解了這些,相信大家對於以下式子理解起來倍感輕鬆。

最後就誘導公式在強調一下這個變,指的是正餘弦互變,正餘切互變。
第五、學法指導
我們在學了這些知識之後,針對他們的題型主要有如下三種:
第一、求值題型,已知一個角的一個三角函式值,求這個角的其他三角函式值;
這類問題,我們需要關注,角的象限或者終邊位置已知,只有一解,角的象限或者終邊需要判斷;也或者,角的三角函式值含有字母,亦或是另一角的三角函式來表示,我們的解法是合理選擇公式,一般思路是按照:“倒-平-倒-商-倒”的順序很容易求解;在開平方的時候,應注意“±”的取捨,有時根據需要分類討論。
第二、化簡題型,目的是簡化運算,要求項數儘量少,次數儘量低,儘量不含分母,儘量不帶根號,儘量為數值。
以上是原則要求,需要關注的是,化簡過程中,不要忽視三角函式的定義區間。
第三、證明題型,本質上是三角恆等式。
常用方法是:
1、從一邊開始,證的另一邊,由繁到簡。
2、左右歸一,證明左右兩邊都等於同一個式子。
3、湊合法,針對題設與結論間的差異,有針對性的變形,以消除差異,即化異為同。
4、比較法,即證明“左邊-右邊=0”,或者“左邊÷右邊=1”
5、分析法,從被證的等式出發,逐步探求使等式成立的充分條件,一直到已知條件或者明顯的事實為止,就可以斷定原等式成立。
常用的技巧:
1、負角化正角,大角化小角,化異為同,常用誘導公式;
2、切割化弦,弦切互化;
3、1的代換,1=sin²α+cos²α=sec²α-tan²α=csc²α-cot²α=tanπ/4;
4、消元和降次;
5、sinα±cosα、sinαcosα,三個式子中,已知其中一個式子,可求其他兩個式子,他隱藏一個條件是:弦的平方和為1。
以上是任意角的三角函式與誘導公式,熟練記憶透徹理解,就在這些口訣上和要點上,相信大家熟讀以上,必定會為三角的學習奠定堅實的基礎。加油!
就以上知識,大家不清楚的地方歡迎大家評論區留言,大黃必將竭盡全力為您解答。感謝!

